前言

前段我读完的ALOAM代码里没有IMU的部分，而原版LOAM代码中其实是有的，除此之外，后面读完的组里的SLAM代码更是使用了IMU、GNSS多种方法进行定位融合和优化约束。虽然代码算是看明白了，但我觉得自己对各种传感器和惯性导航相关的知识很欠缺。之前在网上搜索IMU的时候发现了一篇很好的文章， 看完以后觉得对IMU有了个初步的了解了，可是真到看代码的时候还是对坐标系、IMU互补滤波等问题有很多疑问。上周去快速补了一部分深蓝的多传感融合的课程，觉得里面有的地方并没有讲的很详细，加上自己数学基础差，最后还是看得比较蒙。为了接下来读原版LOAM，以及以后更好地理解多传感器融合的SLAM代码，我决定好好补下相关的知识。这段计划学习以下内容：

  • [x] 惯性导航坐标系与坐标变换
  • [ ] IMU基本知识与数据处理
  • [x] 对组内代码IMU相关的地方加深理解
  • [x] LOAM源码阅读
  • [x] Lego LOAM论文与源码阅读
  • [ ] SLAM综述文章、梳理概念、概率机器人选读
  • [ ] 深蓝多传感器融合课程

常见的定位技术

使用相对测量的技术（Dead Reckoning 航位推测）

里程计

最初只是指轮式里程计，但实际并不是局限于此，现在有所谓视觉里程计、激光里程计，对于SLAM问题我更倾向于致力于获得robot位姿的功能都可以叫做里程计。如果有时间，会总结下里程计相关内容。就轮式里程计而言，优点是成本低，采样率高；缺点是因为累积误差长期精度不行，而且精确受方向估计影响大。

惯性导航

使用惯性传感器（加速度计和陀螺仪）。这种方法是自给的，只需要初始位姿，而不需要参考外部信息。但这种方式因为使用了积分计算，同样有累积误差不随时间收敛的问题。

使用绝对测量的技术（参考系系统)

电子罗盘

使用磁力计提供相对于地球磁场的朝向测量值。它有两个问题，其一是需要已和磁北极与地理北极的夹角，这导致了它是依赖具体位置的；其二是局部磁场易受电线、金属等干扰，这时它会产生不可预测的误差。

活动信标(active beacons)

所谓信标是已知的，这种方式适用于已知环境，能提供准确的定位信息，缺点是安装维护成本高。这里的定位算法有有三边、三角测量、指纹算法等，应用实例主要是无线定位，比如蜂窝网络、UWB，WLAN等。

全球导航卫星系统GNSS

前面已经写过一篇，这里不再赘述。

路标导航

路标是具有区分度的物体或特征，自然物体和人工添加的都可以算，它们应能被载具上相应的传感器检测并区分。

基于地图的定位

  • 已知地图的定位
  • SLAM中的定位
  • 利用GPS的地图匹配定位

惯性导航

基本概念

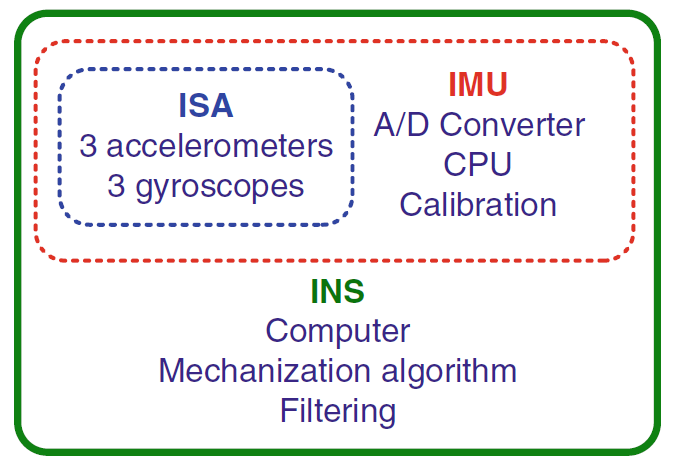
  • 惯性传感器组件 Inertial Sensor Assembly (ISA): （陀螺仪+加速度计）* 3

  • 惯性测量单元 Inertial Measurement Unit (IMU): （陀螺仪+加速度计）* 3 + 相关电路元件

  • 惯性导航系统 Inertial Navigation System (INS): 使用的（陀螺仪+加速度计）* 3 + 处理器 + 算法…

这三者的关系如下图所示：

区分ISA,IMU与INS

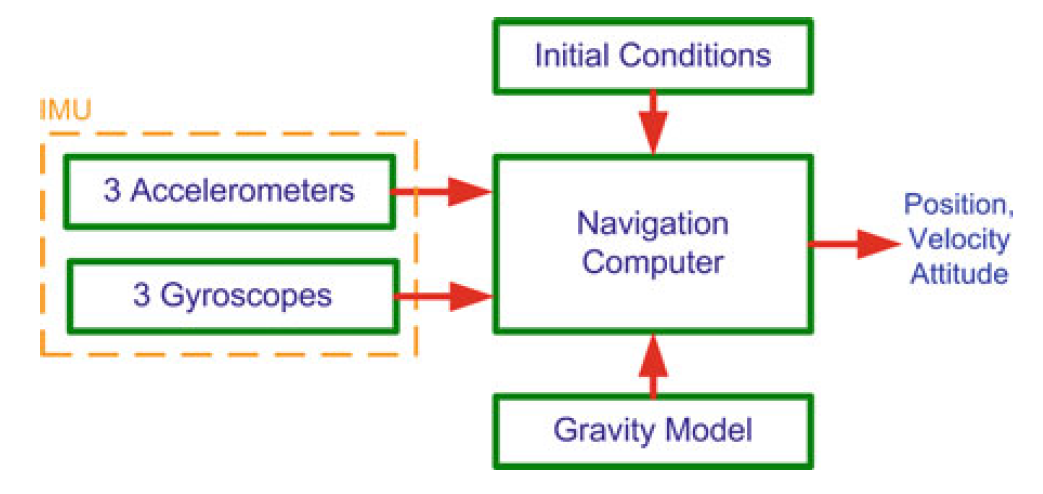
惯性导航系统在已知初始状态的情况下，利用重力模型，处理IMU的测量值，获得位姿、速度等信息，如下图：

INS工作原理

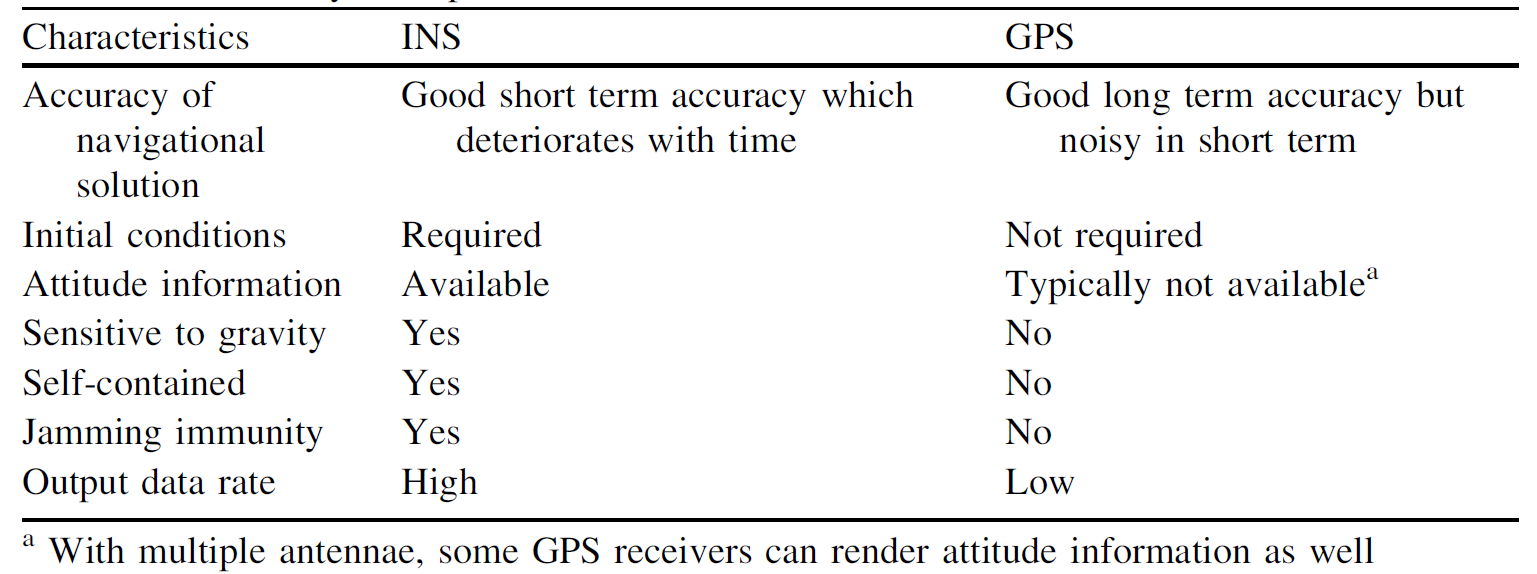
与GPS（GNSS）的对比

GPS与INS对比

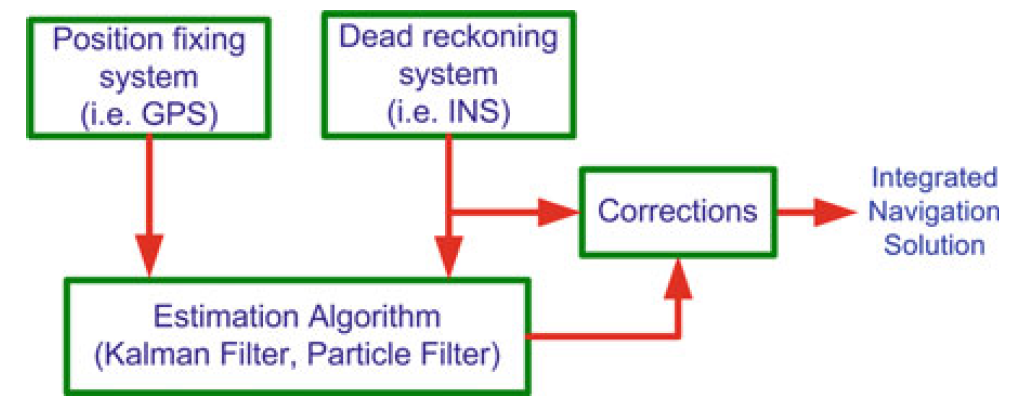
惯导融合卫星

通过上表可看出，很多方面INS与GPS是互补的，我们可以将两种信息融合，以得到更好的精度、帧率与鲁棒性。融合主要通过滤波或AI相关的方法完成，融合方法可以分为松耦合、紧耦合等。

融合

参考系与坐标变换

部分数学基础

表示角速度与速度

kk 坐标系相对 mm 坐标系的角速度，在 pp 坐标系下的表示为：

ωmkp=[ωxωyωz]\omega_{m k}^{p}=\left[\begin{array}{c}\omega_{x} \\ \omega_{y} \\ \omega_{z}\end{array}\right]

kk 相对 pp 下的角速度在 kk 系下的表示，可以拆成 mm 相对于 pp 的角速度在 kk 系的表示加上 kk 相对 mm 的角速度在 kk 系的表示：

ωpkk=ωpmk+ωmkk\boldsymbol{\omega}_{p k}^{k}=\boldsymbol{\omega}_{p m}^{k}+\boldsymbol{\omega}_{m k}^{k}

这里注意上标（在哪个坐标系下表示）必须相同

角速度向量和速度向量对应的反对称矩阵：

ωmkp=[ωxωyωz]⏟Angular velocity vector ⇒Ωmkp=[0−ωzωyωz0−ωx−ωyωx0]⏟Skew-symmetric form of angular the velocity vector \underbrace{\boldsymbol{\omega}_{m k}^{p}=\left[\begin{array}{c}\omega_{x} \\ \omega_{y} \\ \omega_{z}\end{array}\right]}_{\text {Angular velocity vector }} \Rightarrow \underbrace{\Omega_{m k}^{p}=\left[\begin{array}{ccc}0 & -\omega_{z} & \omega_{y} \\ \omega_{z} & 0 & -\omega_{x} \\ -\omega_{y} & \omega_{x} & 0\end{array}\right]}_{\text {Skew-symmetric form of angular the velocity vector }}

vp=[vxvyvz]⏟Velocity vector ⇒Vp=[0−vzvyvz0−vx−vyvx0]⏟Skew-symmetric form of the velocity vector \underbrace{\mathbf{v}^{p}=\left[\begin{array}{c}v_{x} \\ v_{y} \\ v_{z}\end{array}\right]}_{\text {Velocity vector }} \Rightarrow \underbrace{\mathbf{V}^{p}=\left[\begin{array}{ccc}0 & -v_{z} & v_{y} \\ v_{z} & 0 & -v_{x} \\ -v_{y} & v_{x} & 0\end{array}\right]}_{\text {Skew-symmetric form of the velocity vector }}

常用的计算回顾

a⋅b=aTb=bTa\mathbf{a} \cdot \mathbf{b}=\mathbf{a}^{T} \mathbf{b}=\mathbf{b}^{T} \mathbf{a}

a×b=Ab=BTa=−Ba\mathbf{a} \times \mathbf{b}=\mathrm{A} \mathbf{b}=B^{T} \mathbf{a}=-\mathrm{B} \mathbf{a}

[A\mathbf{b}]_{\cross}=\mathrm{AB}-\mathrm{BA}

(a×b)⋅c=a⋅(b×c)=aT Bc(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}=\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})=\mathbf{a}^{T} \mathrm{~B} \mathbf{c}

a×(b×c)=ABc\mathbf{a} \times(\mathbf{b} \times \mathbf{c})=\mathrm{AB} \mathbf{c}

(a×b)×c=ABc−BAc(\mathbf{a} \times \mathbf{b}) \times \mathbf{c}=\mathrm{AB} \mathbf{c}-\mathrm{BA} \mathbf{c}

角速度坐标系变换

kk 相对于 mm 的角速度在 kk 下的表示，转换到 pp下表示，有：

ωmkp=Rkpωmkk\boldsymbol{\omega}_{m k}^{p}=R_{k}^{p} \boldsymbol{\omega}_{m k}^{k}

其对应的反对称矩阵有如下特殊的关系（大雾）：

Ωmkp=RkpΩmkkRpk\Omega_{m k}^{p}=R_{k}^{p} \Omega_{m k}^{k} R_{p}^{k}

地心惯性系 ECI (Earth-Centered Inertial) Frame

所谓惯性系，就是在空间中静止或者匀速运动的坐标系。所有惯性传感器都产生相对于沿其敏感轴解析的惯性坐标系的测量结果。此外，我们还需要利用惯性系计算卫星的位置和环地速度。

地心惯性系一般用 ii 表示，其原点在地球质心，z 轴指向地极conventional terrestrial pole (CTP)， x指向春分点，y根据右手系确定。注意ECI 并不固连在地球上随之转动。

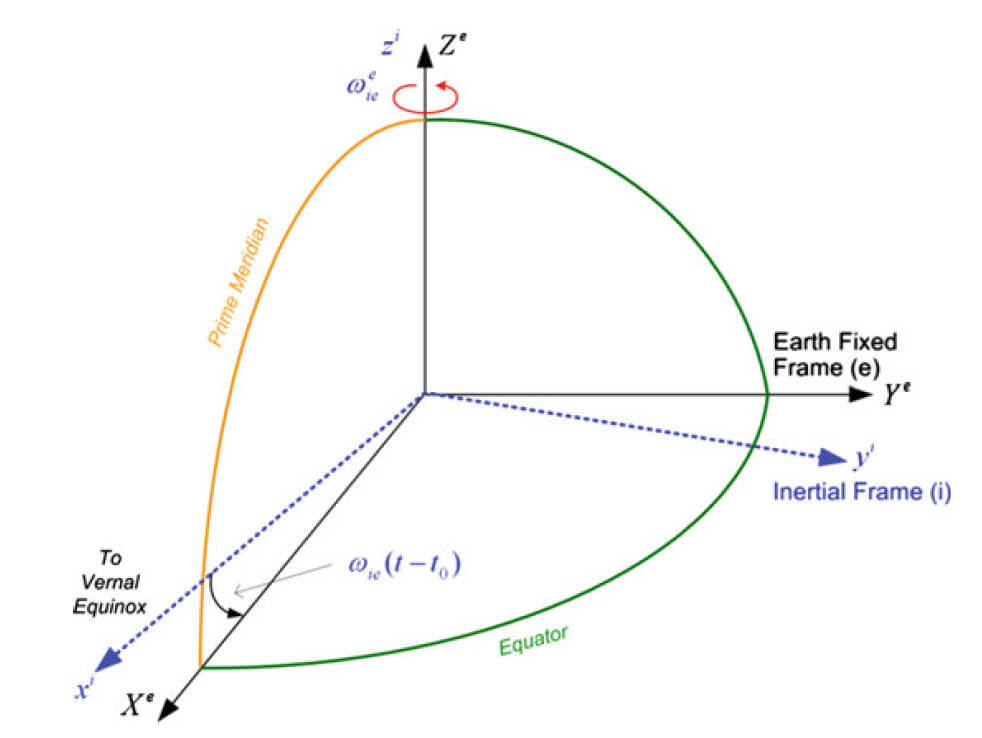
地心固连坐标系 ECEF (Earth-Centered Earth-Fixed) Frame

整体与ECI相似，只是固连在地球上。ECEF通常用 ee 表示其中x 指向赤道面与基准子午线(即格林尼治子午线)的横切面。

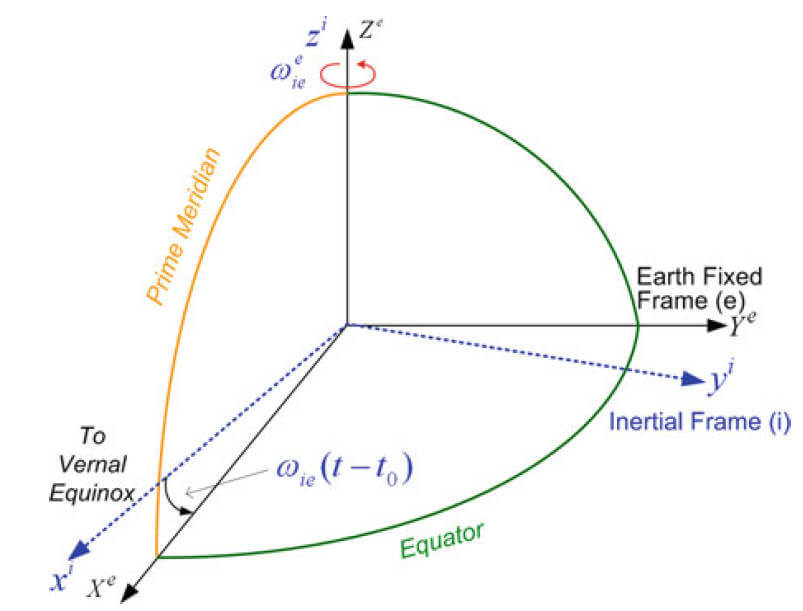
ECI与ECEF如下图：ECI与ECEF

GPS获得的数据坐标系为WGS84，这也是一种ECEF。

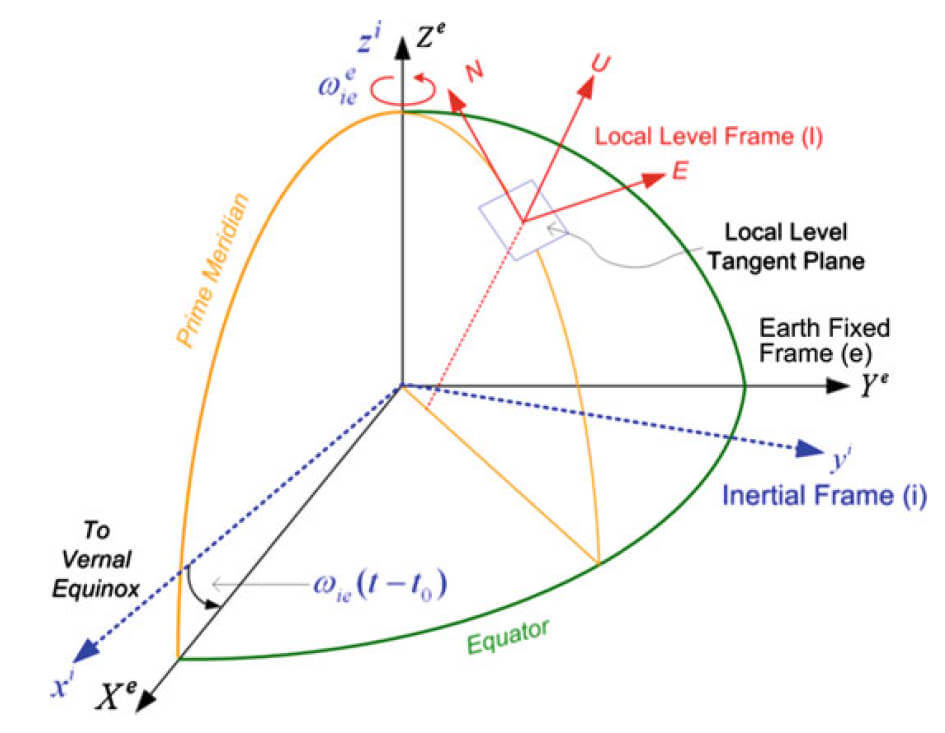
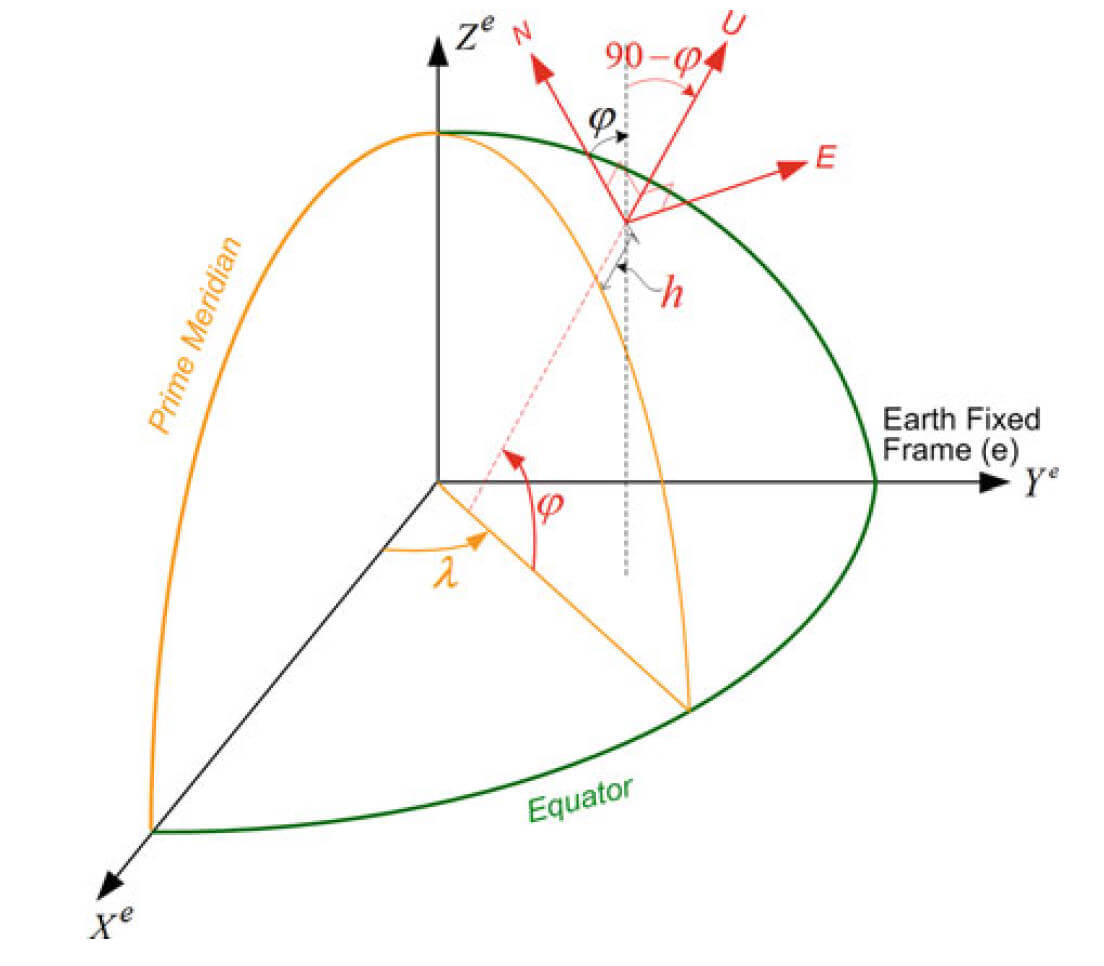
本地级坐标系 LLF (Local-Level Frame) Frame

用来提供地表或近地载具的姿态和速度，也叫 local geodetic frame 或者 navigation frame（导航坐标系）

LLF一般用 ll 表示，根据xyz指向不同，一般有ENU（东北天）和NED（北东地）两种。以ENU为例， 其原点在传感器原点，y指向真北，x指向东方，z指向垂直于当前地表点对应椭球部分的切平面的垂线向上的方向，即指向上方（天）。

本地级坐标系

ENU的LLF中地球重力向量为：

gl=[00−g]T\mathbf{g}^{l}=\left[\begin{array}{lll}0 & 0 & -g\end{array}\right]^{T}

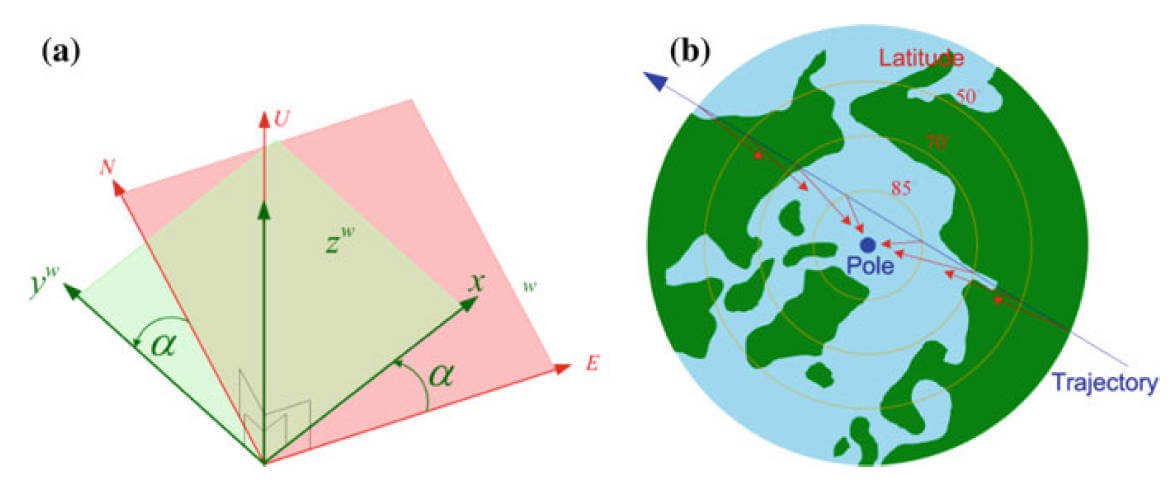
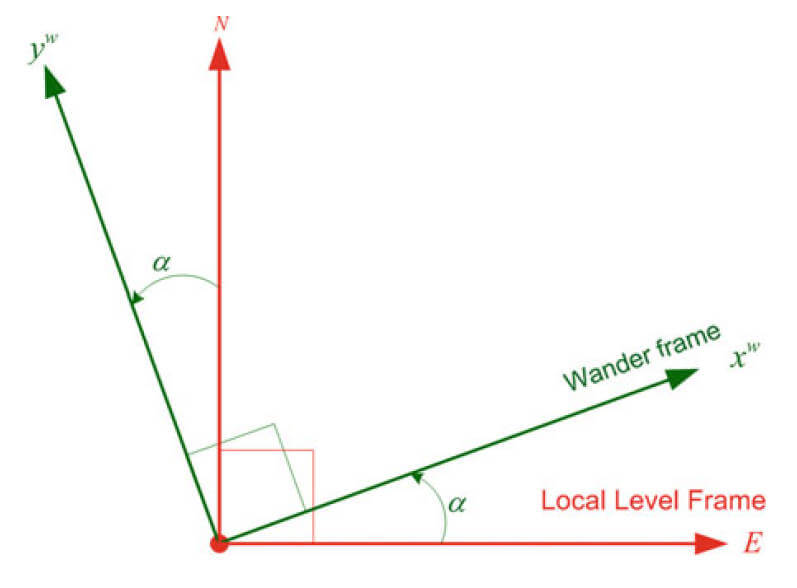
游动坐标系 Wander Frame

LLF中y总是指向真北，这就造成了越靠近极点，LLF系就需要越高的转速以指向北方，尤其在极点处，可以达到无穷速度的奇异情况。为了避免这个问题，Wander Frame不指向真北，而是与北保持一个夹角 α\alpha , 它由下式给出：

α˙=−λ˙sin⁡φ\dot{\alpha}=-\dot{\lambda} \sin \varphi

Wander Frame示意

机身坐标系 Body Frame

大多数情况下，加速度计坐标轴与固连平台的保持一致，这些轴表示了机身坐标系，用 bb 表示。

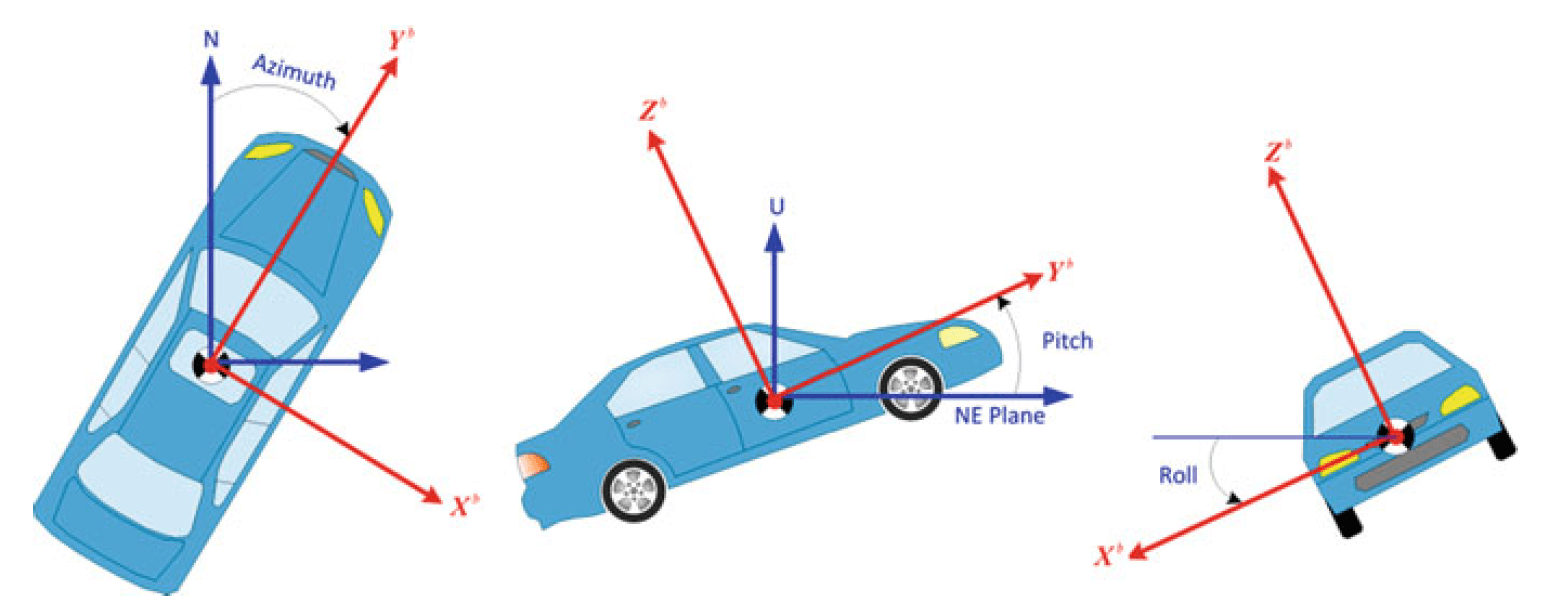
如果Body Frame 原点在载具重心，y指向前方， x指向右方，z指向上方，那么这时y, x, z轴也叫 roll, pitch, yaw轴，因为roll, pitch, yaw角分别根据沿这几个轴的旋转计算的。

rpy角

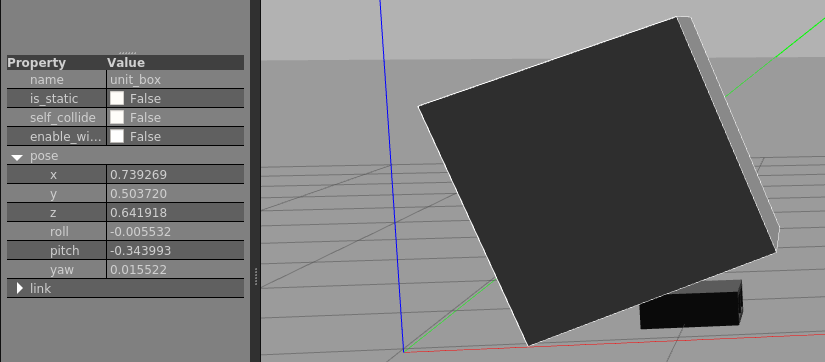
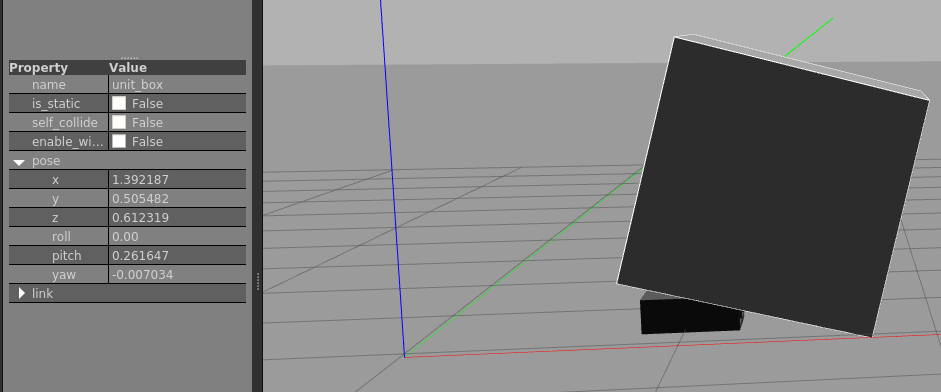
注意LLF和BF原点是同一位置，如果body坐标轴方向按上面规定（不一定都是这样，比如ros的x就指向前方)，则yaw, pitch, roll 角分别指 body frame 沿自己的z, x, y轴分别相对于 ENU frame 的 NU平面、NE平面和NE平面旋转的角度（沿转轴看去按顺时针计算角度）。即如果将导航系作为基系，这时rpy角度其实直接反映了载具的“绝对坐标”，因为是相对本地ENU的，之前自己一直对这个角度有误解。另外，如果将yaw按逆时针角度计算，则将这个角度称为Azimuth角。这个顺逆时针方向不能反，我们可以在gazebo中进行验证：

image-20220409162132744

image-20220409162125165

ROS中body xyz为前左上，分别由rgb颜色表示。可以看出第一种姿态pitch为负，而第二种pitch为正。

rpy角如下所示：

rpy

Euler角

有多种，这里以ZXY为例，认为先沿自己的 zz 转 γ\gamma ，再沿新的 xx 转 β\beta, 最后沿新的 yy 转 α\alpha ，则 α，β，γ\alpha， \beta， \gamma 为欧拉角。由于这相当于沿着先基系的yy 转 α\alpha， 再沿基系 xx 转 β\beta， 最后沿基系 zz 转 γ\gamma ，所以一组Euler角其实对应了一组rpy角，在这里如果以ENU(LLF)为参考系，那么这个α,β,γ\alpha, \beta, \gamma 其实就依次是我们要的 roll,pitch,yawroll, pitch, yaw 。想由姿态矩阵得到欧拉角，就按旋转顺序，从基系看就是左乘起来，从联体看就是右乘起来即可；如果想把姿态矩阵转欧拉角，需要带着各未知角度把R乘开，找到有合适三角关系的元素求解即可。

这里有个很困惑人的地方，似乎由rpy/Euler转换旋转矩阵只能按固定的顺序相乘，即依次相对基系rpy轴，分别转roll, pitch, yaw的角度，不能换顺序（也就是相对联体的相反顺序），因为改变顺序将影响最终的旋转结果。不过我一直没想明白为啥是这个顺序。

对于ZXY的Euler角，可以得到如下关系：

Rbl=[cos⁡ycos⁡r−sin⁡ysin⁡psin⁡r−sin⁡ycos⁡pcos⁡ysin⁡r+sin⁡ysin⁡pcos⁡rsin⁡ycos⁡r+cos⁡ysin⁡psin⁡rcos⁡ycos⁡psin⁡ysin⁡r−cos⁡ysin⁡pcos⁡r−cos⁡psin⁡rsin⁡pcos⁡pcos⁡r]R_{b}^{l}=\left[\begin{array}{ccc}\cos y \cos r-\sin y \sin p \sin r & -\sin y \cos p & \cos y \sin r+\sin y \sin p \cos r \\ \sin y \cos r+\cos y \sin p \sin r & \cos y \cos p & \sin y \sin r-\cos y \sin p \cos r \\ -\cos p \sin r & \sin p & \cos p \cos r\end{array}\right]

p=tan⁡−1{Rbl(3,2)[Rbl(1,2)]2+[Rbl(2,2)]2}p=\tan ^{-1}\left\{\frac{R_{b}^{l}(3,2)}{\sqrt{\left[R_{b}^{l}(1,2)\right]^{2}+\left[R_{b}^{l}(2,2)\right]^{2}}}\right\}

y=−tan⁡−1[Rbl(1,2)Rbl(2,2)]y=-\tan ^{-1}\left[\frac{R_{b}^{l}(1,2)}{R_{b}^{l}(2,2)}\right]

r=−tan⁡−1[Rbl(3,1)Rbl(3,3)]r=-\tan ^{-1}\left[\frac{R_{b}^{l}(3,1)}{R_{b}^{l}(3,3)}\right]

来看下之前读的旋转矩阵与rpy互转的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Utility
{
  public:
    static Eigen::Vector3d R2ypr(const Eigen::Matrix3d &R)
    {
        Eigen::Vector3d n = R.col(0);
        Eigen::Vector3d o = R.col(1);
        Eigen::Vector3d a = R.col(2);

        Eigen::Vector3d ypr(3);
        double y = atan2(n(1), n(0));
        double p = atan2(-n(2), n(0) * cos(y) + n(1) * sin(y));
        double r = atan2(a(0) * sin(y) - a(1) * cos(y), -o(0) * sin(y) + o(1) * cos(y));
        ypr(0) = y;
        ypr(1) = p;
        ypr(2) = r;

        return ypr / M_PI * 180.0;
    }

    template <typename Derived>
    static Eigen::Matrix<typename Derived::Scalar, 3, 3> ypr2R(const Eigen::MatrixBase<Derived> &ypr)
    {
        typedef typename Derived::Scalar Scalar_t;

        Scalar_t y = ypr(0) / 180.0 * M_PI;
        Scalar_t p = ypr(1) / 180.0 * M_PI;
        Scalar_t r = ypr(2) / 180.0 * M_PI;

        Eigen::Matrix<Scalar_t, 3, 3> Rz;
        Rz << cos(y), -sin(y), 0,
            sin(y), cos(y), 0,
            0, 0, 1;

        Eigen::Matrix<Scalar_t, 3, 3> Ry;
        Ry << cos(p), 0., sin(p),
            0., 1., 0.,
            -sin(p), 0., cos(p);

        Eigen::Matrix<Scalar_t, 3, 3> Rx;
        Rx << 1., 0., 0.,
            0., cos(r), -sin(r),
            0., sin(r), cos(r);

        return Rz * Ry * Rx;
    }
};

可以看到转已知rpy,转姿态矩阵R是相对基系的x, y, z 依次转roll, pitch yaw获得；根据上面说的，也可以理解为相对联体坐标系转的yaw, pitch, roll。由于这里按zyx的顺序，可以推出body frame的x是向前的，y是向左的，这就与ROS中的一致了。至于上面代码中的已知姿态矩阵R转rpy角，则要按ZYX Euler角的顺序计算了，和上面给出的公式不同。

Eigen从旋转矩阵得到欧拉角/rpy角：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Matrix3f m;
m = AngleAxisf(0.25*M_PI, Vector3f::UnitX())
    * AngleAxisf(0.5*M_PI, Vector3f::UnitY())
    * AngleAxisf(0.33*M_PI, Vector3f::UnitZ());

cout << "original rotation:" << endl;
cout << m << endl << endl;

Vector3f ea = m.eulerAngles(0, 1, 2);  // 得到右乘的**Euler角**，旋转顺序为先沿x, 再沿新的y, 再沿新的z
// ea = m.eulerAngles(2, 1, 0);  // 这样得到的角的顺序就是roll, pitch, yaw
// 总结
// rotation_matrix.eulerAngles 按右乘顺序输入坐标轴，得到的是欧拉角顺序；按左乘顺序输入坐标轴，得到的是rpy顺序。
cout << "to Euler angles:" << endl;
cout << ea << endl << endl;

Matrix3f n;
n = AngleAxisf(ea[0], Vector3f::UnitX())
    * AngleAxisf(ea[1], Vector3f::UnitY())
    * AngleAxisf(ea[2], Vector3f::UnitZ()); 

cout << "recalc original rotation:" << endl;
cout << n << endl;
// m 与 n 输出相同（有一点点误差）

注意得到角度后要对其标准化，比如yaw归到$-\pi \sim \pi $, 而pitch与roll则应在 −π2∼π2-\frac{\pi}{2} \sim \frac{\pi}{2}

轨道坐标系 Orbital Coordinate System

这个主要是GPS用到，了解即可。

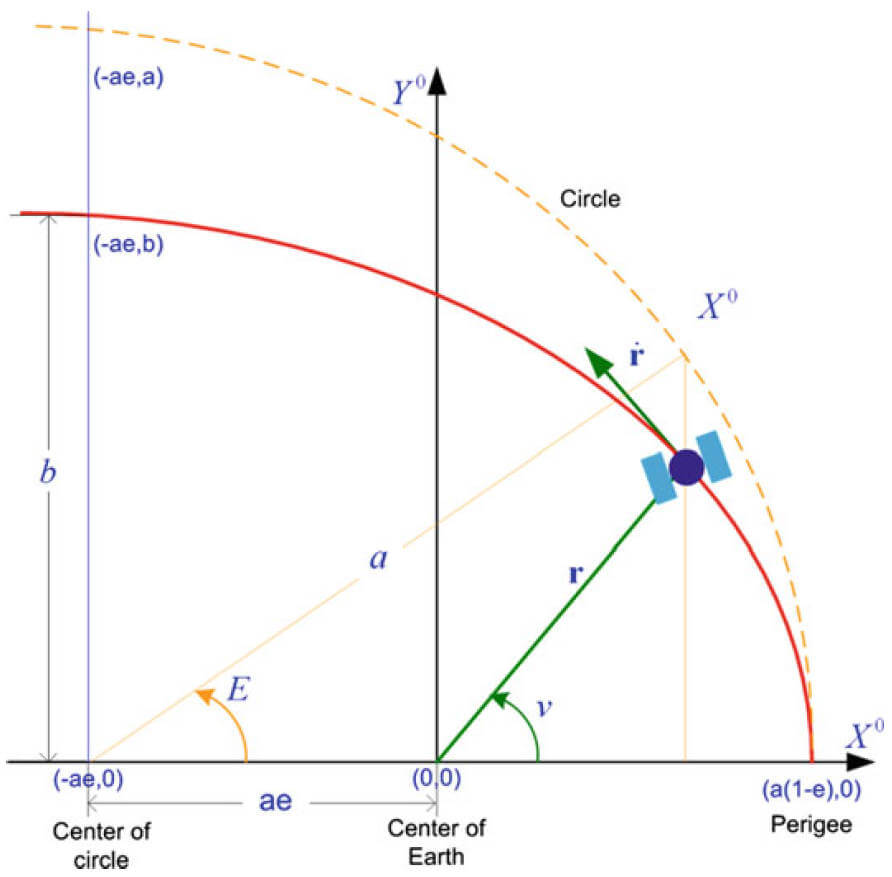
原点位于与地球质量中心重合的椭圆轨道的焦点上。y轴指向下行节点，与轨道椭圆的短轴平行, x轴沿着卫星椭圆轨道的长轴指向近地点(距离地球中心最近的轨道上的点)，z 垂直于轨道平面，如下图：

轨道坐标系

坐标变换

ECEF转ECI

ECEF转ECI

Rei=[cos⁡ωet−sin⁡ωet0sin⁡ωetcos⁡ωet0001]R_{e}^{i}=\left[\begin{array}{ccc}\cos \omega_{e} t & -\sin \omega_{e} t & 0 \\ \sin \omega_{e} t & \cos \omega_{e} t & 0 \\ 0 & 0 & 1\end{array}\right]

LLF转ECEF

LLF转ECEF

Rle=[cos⁡(−λ−90)sin⁡(−λ−90)0−sin⁡(−λ−90)cos⁡(−λ−90)0001][1000cos⁡(φ−90)sin⁡(φ−90)0−sin⁡(φ−90)cos⁡(φ−90)]R_{l}^{e}=\left[\begin{array}{ccc}\cos (-\lambda-90) & \sin (-\lambda-90) & 0 \\ -\sin (-\lambda-90) & \cos (-\lambda-90) & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos (\varphi-90) & \sin (\varphi-90) \\ 0 & -\sin (\varphi-90) & \cos (\varphi-90)\end{array}\right]

Rle=[−sin⁡λ−sin⁡φcos⁡λcos⁡φcos⁡λcos⁡λ−sin⁡φsin⁡λcos⁡φsin⁡λ0cos⁡φsin⁡φ]R_{l}^{e}=\left[\begin{array}{ccc}-\sin \lambda & -\sin \varphi \cos \lambda & \cos \varphi \cos \lambda \\ \cos \lambda & -\sin \varphi \sin \lambda & \cos \varphi \sin \lambda \\ 0 & \cos \varphi & \sin \varphi\end{array}\right]

Wander Frame转LLF

Wander Frame转LLF

Rwl=[cos⁡(−α)sin⁡(−α)0−sin⁡(−α)cos⁡(−α)0001]R_{w}^{l}=\left[\begin{array}{ccc}\cos (-\alpha) & \sin (-\alpha) & 0 \\ -\sin (-\alpha) & \cos (-\alpha) & 0 \\ 0 & 0 & 1\end{array}\right]

Rwl=[cos⁡α−sin⁡α0sin⁡αcos⁡α0001]R_{w}^{l}=\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1\end{array}\right]

Wander转ECEF

Rwe=[−sin⁡λcos⁡α−cos⁡λsin⁡φsin⁡αsin⁡λsin⁡α−cos⁡λsin⁡φcos⁡αcos⁡λcos⁡φcos⁡λcos⁡α−sin⁡λsin⁡φsin⁡α−cos⁡λsin⁡α−sin⁡λsin⁡φcos⁡αsin⁡λcos⁡φcos⁡φsin⁡αcos⁡φcos⁡αsin⁡φ]R_{w}^{e}=\left[\begin{array}{ccc}-\sin \lambda \cos \alpha-\cos \lambda \sin \varphi \sin \alpha & \sin \lambda \sin \alpha-\cos \lambda \sin \varphi \cos \alpha & \cos \lambda \cos \varphi \\ \cos \lambda \cos \alpha-\sin \lambda \sin \varphi \sin \alpha & -\cos \lambda \sin \alpha-\sin \lambda \sin \varphi \cos \alpha & \sin \lambda \cos \varphi \\ \cos \varphi \sin \alpha & \cos \varphi \cos \alpha & \sin \varphi\end{array}\right]

Rwe=RleRwlR_{w}^{e}=R_{l}^{e} R_{w}^{l}

Body转LLF

注意这里是ZXY Euler。

Rbl=[cos⁡ycos⁡r−sin⁡ysin⁡psin⁡r−sin⁡ycos⁡pcos⁡ysin⁡r+sin⁡ysin⁡pcos⁡rsin⁡ycos⁡r+cos⁡ysin⁡psin⁡rcos⁡ycos⁡psin⁡ysin⁡r−cos⁡ysin⁡pcos⁡r−cos⁡psin⁡rsin⁡pcos⁡pcos⁡r]R_{b}^{l}=\left[\begin{array}{ccc}\cos y \cos r-\sin y \sin p \sin r & -\sin y \cos p & \cos y \sin r+\sin y \sin p \cos r \\ \sin y \cos r+\cos y \sin p \sin r & \cos y \cos p & \sin y \sin r-\cos y \sin p \cos r \\ -\cos p \sin r & \sin p & \cos p \cos r\end{array}\right]

p=tan⁡−1{Rbl(3,2)[Rbl(1,2)]2+[Rbl(2,2)]2}p=\tan ^{-1}\left\{\frac{R_{b}^{l}(3,2)}{\sqrt{\left[R_{b}^{l}(1,2)\right]^{2}+\left[R_{b}^{l}(2,2)\right]^{2}}}\right\}

y=−tan⁡−1[Rbl(1,2)Rbl(2,2)]y=-\tan ^{-1}\left[\frac{R_{b}^{l}(1,2)}{R_{b}^{l}(2,2)}\right]

r=−tan⁡−1[Rbl(3,1)Rbl(3,3)]r=-\tan ^{-1}\left[\frac{R_{b}^{l}(3,1)}{R_{b}^{l}(3,3)}\right]

Body转ECEF和ECI

Rbe=RleRblR_{b}^{e}=R_{l}^{e} R_{b}^{l}

Rbi=ReiRbeR_{b}^{i}=R_{e}^{i} R_{b}^{e}

微分变换

微分旋转

如果认为欧拉角很小，有如下近似：

cos⁡θ≈1,sin⁡θ≈θ\cos \theta \approx 1, \sin \theta \approx \theta

则变换后的d相对于基系a有:

Rda≈[1−γαγ1−β−αβ1]R_{d}^{a} \approx\left[\begin{array}{ccc}1 & -\gamma & \alpha \\ \gamma & 1 & -\beta \\ -\alpha & \beta & 1\end{array}\right]

Rda=[100010001]+[0−γαγ0−β−αβ0]R_{d}^{a}=\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]+\left[\begin{array}{ccc}0 & -\gamma & \alpha \\ \gamma & 0 & -\beta \\ -\alpha & \beta & 0\end{array}\right]

Rda=I+ΨTR_{d}^{a}=I+\Psi^{T}

变换矩阵对时间的微分

令 RkmR_k^m 为 kk 在 mm 下的表示，则有：

R˙km=lim⁡δt→0δRkmδt\dot{R}_{k}^{m}=\lim _{\delta t \rightarrow 0} \frac{\delta R_{k}^{m}}{\delta t}

R˙km=lim⁡δt→0Rkm(t+δt)−Rkm(t)δt\dot{R}_{k}^{m}=\lim _{\delta t \rightarrow 0} \frac{R_{k}^{m}(t+\delta t)-R_{k}^{m}(t)}{\delta t}

注意到 t+δtt+\delta t 时刻的R可以看作 t时刻之后 mm 又旋转了一点点，这可以表示为：

Rkm(t+δt)=δRmRkm(t)R_{k}^{m}(t+\delta t)=\delta R^{m} R_{k}^{m}(t)

根据微分旋转， 有

δRm=I+Ψm\delta R^{m}=I+\Psi^{m}

代回到上面式子，有

R˙km=lim⁡δt→0(I+Ψm)Rkm(t)−Rkm(t)δtR˙km=lim⁡δt→0(I+Ψm−I)Rkm(t)δtR˙km=lim⁡δt→0ΨmRkm(t)δtR˙km=(lim⁡δt→0Ψmδt)Rkm(t)\begin{aligned} \dot{R}_{k}^{m} &=\lim _{\delta t \rightarrow 0} \frac{\left(I+\Psi^{m}\right) R_{k}^{m}(t)-R_{k}^{m}(t)}{\delta t} \\ \dot{R}_{k}^{m} &=\lim _{\delta t \rightarrow 0} \frac{\left(I+\Psi^{m}-I\right) R_{k}^{m}(t)}{\delta t} \\ \dot{R}_{k}^{m} &=\lim _{\delta t \rightarrow 0} \frac{\Psi^{m} R_{k}^{m}(t)}{\delta t} \\ \dot{R}_{k}^{m} &=\left(\lim _{\delta t \rightarrow 0} \frac{\Psi^{m}}{\delta t}\right) R_{k}^{m}(t) \end{aligned}

当 δt→0\delta_t \rightarrow 0 时, Ψm/δt\Psi^{m} / \delta t 是 mm 相对于 kk 的角速度矢量对应的反对称矩阵

lim⁡δt→0Ψmδt=Ωmkm\lim _{\delta t \rightarrow 0} \frac{\Psi^{m}}{\delta t}=\Omega_{m k}^{m}

最终有:

R˙km=ΩmkmRkm\dot{R}_{k}^{m}=\Omega_{m k}^{m} R_{k}^{m}

最后借用前面大雾的 Ωmkm=RkmΩmkkRmk\Omega_{m k}^{m}=R_{k}^{m} \Omega_{m k}^{k} R_{m}^{k}, 最终有:

R˙km=RkmΩmkk\dot{R}_{k}^{m}=R_{k}^{m} \Omega_{m k}^{k}

可以看出,旋转矩阵对时间的微分与表征两坐标系相对旋转的角速度向量有关,如果我们已知 RbiR_b^i, 那就可以使用陀螺仪输出的角速度 Ωibb\Omega_{i b}^{b} 更新旋转的变化量。

惯性系中位置向量对时间的微分

已知 ri=Rbirb\mathbf{r}^{i}=R_{b}^{i} \mathbf{r}^{b}, 两边同时取微分,有:

r˙i=R˙birb+Rbir˙b\dot{\mathbf{r}}^{i}=\dot{R}_{b}^{i} \mathbf{r}^{b}+R_{b}^{i} \dot{\mathbf{r}}^{b}

根据旋转矩阵微分的推导结果,有:

r˙i=(RbiΩibb)rb+Rbir˙b\dot{\mathbf{r}}^{i}=\left(R_{b}^{i} \Omega_{i b}^{b}\right) \mathbf{r}^{b}+R_{b}^{i} \dot{\mathbf{r}}^{b}

r˙i=Rbi(r˙b+Ωibbrb)(科氏方程)\dot{\mathbf{r}}^{i}=R_{b}^{i}\left(\dot{\mathbf{r}}^{b}+\Omega_{i b}^{b} \mathbf{r}^{b}\right) (科氏方程)

这样就得到了机身坐标系相对惯性坐标系的速度向量.

惯性系中速度向量对时间的微分

对上面的速度向量微分,有:

r¨i=R˙bir˙b+Rbir¨b+R˙biΩibbrb+(Ω˙ibbrb+Ωibbr˙b)Rbir¨i=R˙bir˙b+Rbir¨b+R˙biΩibbrb+RbiΩ˙ibbrb+RbiΩibbr˙b\begin{aligned} \ddot{\mathbf{r}}^{i} &=\dot{R}_{b}^{i} \dot{\mathbf{r}}^{b}+R_{b}^{i} \ddot{\mathbf{r}}^{b}+\dot{R}_{b}^{i} \Omega_{i b}^{b} \mathbf{r}^{b}+\left(\dot{\Omega}_{i b}^{b} \mathbf{r}^{b}+\Omega_{i b}^{b} \dot{\mathbf{r}}^{b}\right) R_{b}^{i} \\ \ddot{\mathbf{r}}^{i} &=\dot{R}_{b}^{i} \dot{\mathbf{r}}^{b}+R_{b}^{i} \ddot{\mathbf{r}}^{b}+\dot{R}_{b}^{i} \Omega_{i b}^{b} \mathbf{r}^{b}+R_{b}^{i} \dot{\Omega}_{i b}^{b} \mathbf{r}^{b}+R_{b}^{i} \Omega_{i b}^{b} \dot{\mathbf{r}}^{b} \end{aligned}

同样代入上面新得到的结果,有:

r¨i=Rbi(r¨b+2Ωibbr˙b+Ω˙ibbrb+ΩibbΩibbrb)\ddot{\mathbf{r}}^{i}=R_{b}^{i}\left(\ddot{\mathbf{r}}^{b}+2 \Omega_{i b}^{b} \dot{\mathbf{r}}^{b}+\dot{\Omega}_{i b}^{b} \mathbf{r}^{b}+\Omega_{i b}^{b} \Omega_{i b}^{b} \mathbf{r}^{b}\right)

这样就得到了机身坐标系相对惯性坐标系的加速度向量.

参考

[1] IMU与惯性导航基础知识介绍

[2] Noureldin A, Karamat T B, Georgy J. Fundamentals of inertial navigation, satellite-based positioning and their integration[J]. 2013.