IMU与惯性导航知识（二）

IMU原理

加速度计

加速度计输出为补偿a-g后的值f（相反力/m），称为比力：

$$\mathbf{f}=\mathbf{a}-\mathbf{g}$$

其中a为实际加速度。

根据a可以被位置矢量r表示 ：

\mathbf{a}=\left.\frac{d^{2} \mathbf{r}}{d t^{2}}\right|_{i}=\ddot{\mathbf{r}}$$。 已知引力场向量为： $$\overline{\mathbf{g}}=\mathbf{g}+\Omega_{i e} \Omega_{i e} \mathbf{r}

最终得到比力和位置矢量的关系：

$$\mathbf{f}=\left.\frac{d^{2} \mathbf{r}}{d t^{2}}\right|_{i}-\mathbf{g}-\Omega_{i e} \Omega_{i e} \mathbf{r}$$

陀螺仪

测量body相对惯性系的角速度在body frame下的值:

$$\omega_{i b}^{b}=\omega_{i e}^{b}+\omega_{e n}^{b}+\omega_{n b}^{b}$$

计算方法

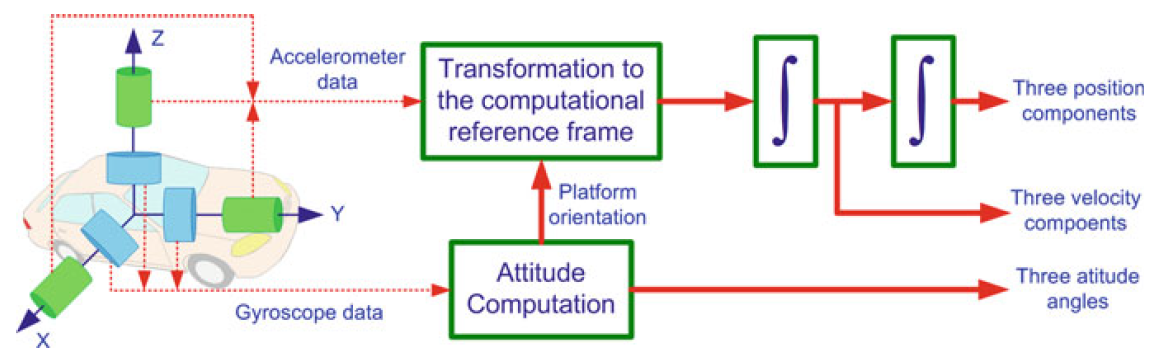
IMU误差

系统误差

系统误差可以在标定后进行补偿。

Bias Offset

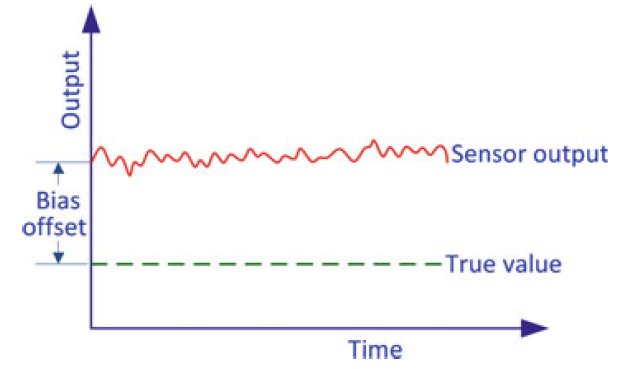
Scale Factor Error

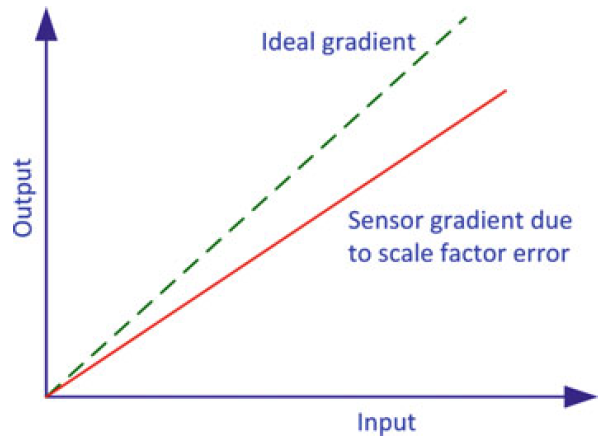
Non-linearity

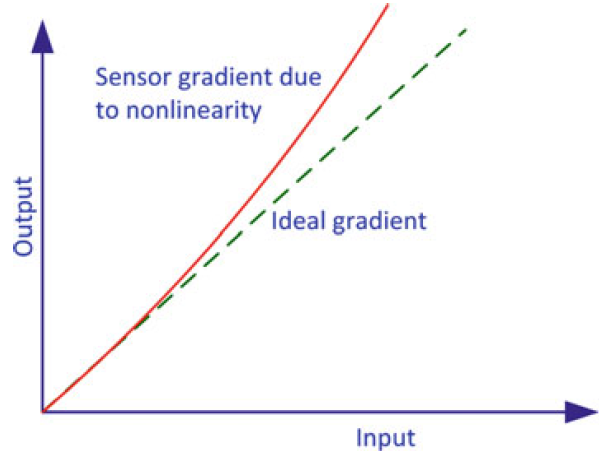
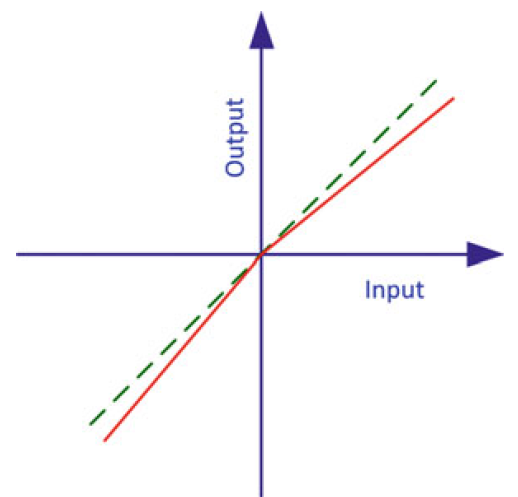
不对称与死区

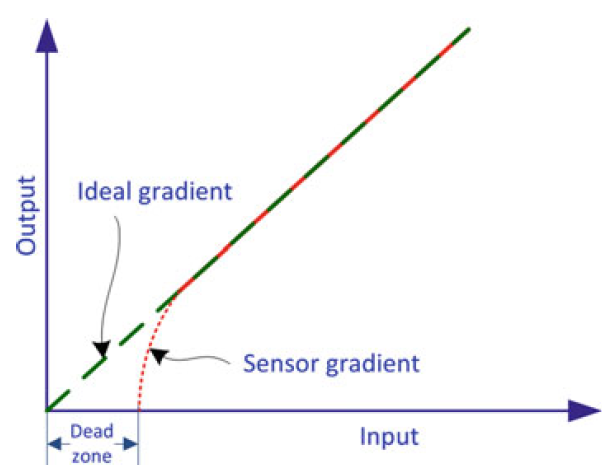
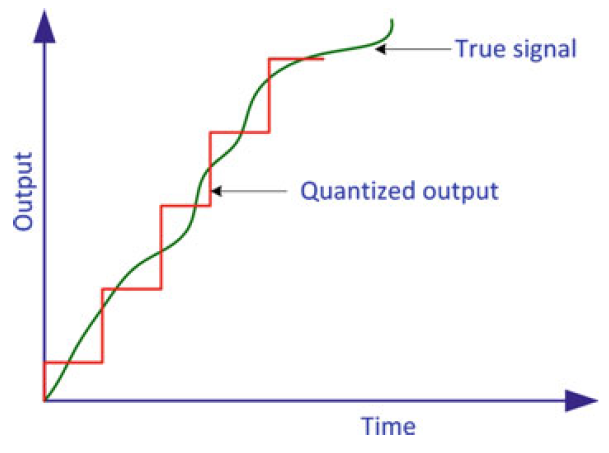
Quantization Error

来自模数转换

Non-orthogonality Error 非正交误差

传感器各敏感轴不垂直

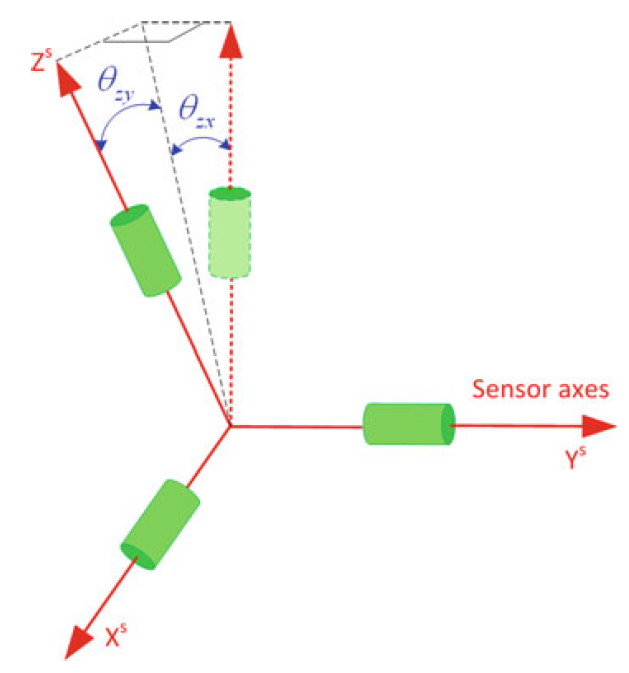
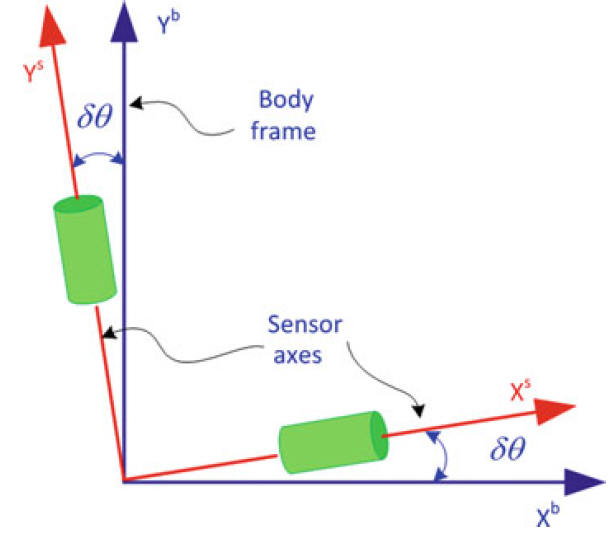
Non-orthogonality Error 安装误差

随机误差

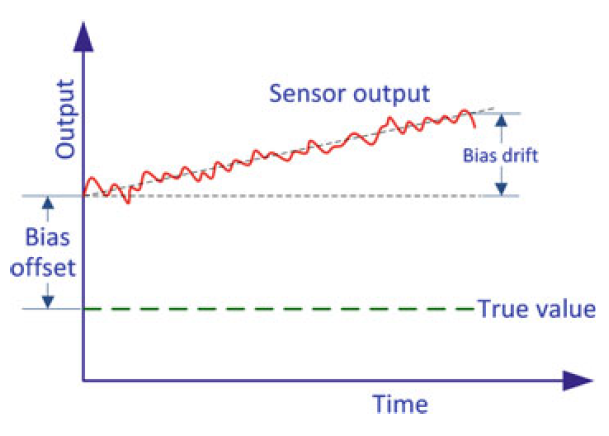
Run-to-Run Bias Offset

bias offset每次都变，不可重复。

Bias Drift/ Scale Factor Instability

单次运行bias / scale factor 不断变动

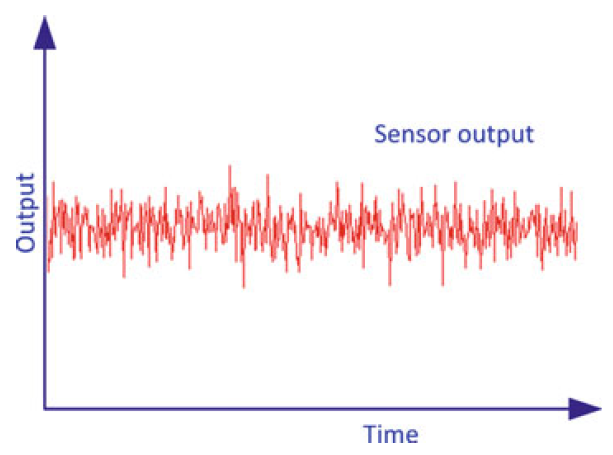
white errors

IMU实际测量模型

陀螺仪测量模型

$$\tilde{\boldsymbol{\omega}}_{i b}^{b}=\boldsymbol{\omega}_{i b}^{b}+\mathbf{b}_{g}+S \boldsymbol{\omega}_{i b}^{b}+N \boldsymbol{\omega}_{i b}^{b}+\boldsymbol{\varepsilon}_{g}$$

$$\tilde{\omega}_{i b}^{b} \quad \text { 是陀螺仪角速度测量值 }(\mathrm{deg} / \mathrm{h})$$

$$\boldsymbol{\omega}_{i b}^{b} \quad \text { 是角速度真值 }(\mathrm{deg} / \mathrm{h})$$

$$\mathbf{b}_{g} \quad \text { bias }(\mathrm{deg} / \mathrm{h})$$

$$S_{g} \quad scale\_factor$$

$$N_{g} \quad \text{代表非正交误差的矩阵}$$

$$\boldsymbol{\varepsilon}_{g} \quad \text { 陀螺仪噪声 }(\mathrm{deg} / \mathrm{h})$$

$$N_{g}=\left[\begin{array}{ccc}1 & \theta_{g, x y} & \theta_{g, x z} \\ \theta_{g, y x} & 1 & \theta_{g, y z} \\ \theta_{g, z x} & \theta_{g, z y} & 1\end{array}\right]$$

$$S_{g}=\left[\begin{array}{ccc}s_{g, x} & 0 & 0 \\ 0 & s_{g, y} & 0 \\ 0 & 0 & s_{g, z}\end{array}\right]$$

加速度计测量模型

$$\tilde{\mathbf{f}}^{b}=\mathbf{f}^{\mathbf{b}}+\mathbf{b}_{\mathbf{a}}+\mathbf{S}_{1} \mathbf{f}+\mathbf{S}_{\mathbf{2}} \mathbf{f}^{2}+\mathbf{N}_{\mathbf{a}} \mathbf{f}+\delta \mathbf{g}+\mathbf{\varepsilon}_{\mathbf{a}}$$

$$\mathbf{f}^{b} 加速度计加速度测量值$$

$$\mathbf{b}_{a} 加速度真值$$

$$S_{1} 线性scale\_factor$$

$$S_{2} 非线性scale\_factor$$

$$N_{a} 代表非正交矩阵的误差$$

$$\delta \mathbf{g} 异常的重力向量（如与理论重力的偏离）$$

$$\boldsymbol{\varepsilon}_{a} 加速度计噪声$$

$$N_{a}=\left[\begin{array}{ccc}1 & \theta_{a, x y} & \theta_{a, x z} \\ \theta_{a, y x} & 1 & \theta_{a, y z} \\ \theta_{a, z x} & \theta_{a, z y} & 1\end{array}\right]$$

$$S_{1}=\left[\begin{array}{ccc}s_{1, x} & 0 & 0 \\ 0 & s_{1, y} & 0 \\ 0 & 0 & s_{1, z}\end{array}\right]$$

$$S_{2}=\left[\begin{array}{ccc}s_{2, x} & 0 & 0 \\ 0 & s_{2, y} & 0 \\ 0 & 0 & s_{2, z}\end{array}\right]$$

IMU初始化与校准

因为INS得到速度、姿态或位置需要通过积分来完成，所以需要指定一个初值。

指定速度与位置的过程称为初始化（initialization)，指定姿态初值的过程称为校准（alignment)。

位速初始化

如果有外部传感器如GPS，可以直接用外部传感值初始化位置；如果没有，可以用移动前的位置初始化（如SLAM建的全局地图）。

还有一种情况是已知位置先验，则可以用先验初始化。

如果有机器人静止，速度可以初始化为0； 如果机器人运动且有外部传感，速度可以通过如GPS的方式初始化。

姿态校准

1. 先通过加速度计获取pitch和roll

$$\begin{aligned} \mathbf{f}^{b} &=R_{l}^{b}\left(-\mathbf{g}^{l}\right) =\left(R_{b}^{l}\right)^{T}\left(-\mathbf{g}^{l}\right) \end{aligned}$$

$$\mathbf{g}^{l}=\left[\begin{array}{lll}0 & 0 & -g\end{array}\right]^{T}$$

$$\mathbf{f}^{b} = \left[\begin{array}{l}f_{x} \\ f_{y} \\ f_{z}\end{array}\right]$$

根据上式可以得到 roll 和 pitch

2. 再通过陀螺仪获取yaw。

$$\omega_{i b}^{b}=\omega_{i e}^{b}+\omega_{e b}^{b}$$

$$\begin{aligned} \omega_{i b}^{b} &=\omega_{i e}^{b}+0 \\ \omega_{i b}^{b} &=R_{e}^{b} \omega_{i e}^{e} \\ \omega_{i b}^{b} &=R_{l}^{b} R_{e}^{l} \omega_{i e}^{e} \\ \omega_{i b}^{b} &=\left(R_{b}^{l}\right)^{T}\left(R_{l}^{e}\right)^{T} \omega_{i e}^{e} \end{aligned}$$

$$\omega_{i e}^{e}=\left[\begin{array}{lll}0 & 0 & \omega_{e}\end{array}\right]^{T}$$

$\omega_{e}$ 大约为15.04 deg/h。

因为roll,pitch已知，可以算出yaw。

如果机器人在接近平面的位置，可以通过小角近似roll与pitch.

最后，如果IMU比较low，不能用上面的方法算yaw角，噪声量级掩盖自转。这时可以用罗盘，磁力计，GPS等给出yaw角。

IMU标定

//TODO

ros imu

//TODO

参考

[1] Noureldin A, Karamat T B, Georgy J. Fundamentals of inertial navigation, satellite-based positioning and their integration[J]. 2013.