LOAM中的数学推导

前言

之前看的A-LOAM代码把优化交给了ceres，而最初自己看论文时也只明白要优化变量和原理，并没有自己推导细节。后来在总结LOAM代码时，突然发现自己完全不知道这部分应该怎么手写，因此有必要自己来一遍数学推导。

非标量求导

上学期上课时我就对包含向量/矩阵的求导一头雾水，搞不清楚怎么求，每次都是上网找别人写的往上套。最近看 numerical optimization 回炉SLAM用到的非线性优化，各种求导又让我无语了。上网研究了一下，算是找到一些不错的资料。

首先要明白，矩阵求导是有不同的使用习惯的，主要有两种：分子布局和分母布局，后者也称混合布局。

对于分子布局，向量y对标量x求导，得到的是列向量，标量y对向量x求导，得到的是行向量；

对于分母布局，向量y对标量x求导，得到的是行向量，标量y对向量x求导，得到的是列向量；

其他详细内容需要参考 wiki 。

根据矩阵求导术（下） - 知乎 中所说，机器学习/优化中的梯度矩阵常用分母布局，而控制论等领域中的Jacobian矩阵采用分子布局，后者的例子有 numerical optimization 的最小二乘部分（其他没看）以及LOAM的代码。实际上，还有两种规定混用的，似乎Matrix Cookbook就是这样。另外，SLAM十四讲也比较奇怪，它在附录中规定了分子布局，但它前面用的雅可比$J$似乎是反的（???)

如果仅仅是首次看矩阵求导，我觉得下面的文章思想十分不错，它是按分母布局来的：

• 矩阵求导术（上） - 知乎
• 矩阵求导术（下） - 知乎

为了能形成一种长期快速使用的方法，则 Matrix_Derivatives下面的PDF手册很好，可配合 Matrix Cookbook食用。注意，关于行列这些，这个手册有自己的规范。

最后，矩阵求导其实本没有所谓链式法则，但在一些情况下也可以根据相应布局来使用，这部分还没有深入研究，可以参考wiki和这里。对于分子布局的向量对向量求导，可以沿用以前的链式顺序。

高斯牛顿法

最小二乘问题

$$\min _{\boldsymbol{x}} F(\boldsymbol{x})=\frac{1}{2}\|f(\boldsymbol{x})\|_{2}^{2}$$

$$r_{j}(x)=\epsilon_{j}=\phi\left(x ; t_{j}\right)-y_{j}$$

比如让 $$f(x)=r(x)$$

则将error以最小平方来优化，原理是假设观测数据与预测数据之差符合正态分布，找最好的模型参数应该能让观测数据与产生的预测数据之差在其正态分布中的可能性最大，即寻找一组参数使之最可能产生现在的已有数据，这就是一个最大似然估计问题。假设各残差项相互独立，则有：

$$p(y ; x, \sigma)=\prod_{j=1}^{m} g_{\sigma}\left(\epsilon_{j}\right)=\prod_{j=1}^{m} g_{\sigma}\left(\phi\left(x ; t_{j}\right)-y_{j}\right)$$

由于假设正态分布，有：

$$g_{\sigma}(\epsilon)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\epsilon^{2}}{2 \sigma^{2}}\right)$$

得出问题实质就是给定正态分布和一组数据，就是估计参数使下面$p$最大化:

$$p(y ; x, \sigma)=\left(2 \pi \sigma^{2}\right)^{-m / 2} \exp \left(-\frac{1}{2 \sigma^{2}} \sum_{j=1}^{m}\left[\phi\left(x ; t_{j}\right)-y_{j}\right]^{2}\right)$$

这就要将括号里的平方项最小化，这就是前面最小平方差的来源。

非线性最小二乘

如果上面的$f(x)$ 为简单的线性函数，则可以直接求导找到极值，但有时则没那么好求解，引用十四讲中的：

求解这个方程需要我们知道关于目标函数的全局性质，而通常这是不大可能的。对于不方便直接求解的最小二乘问题，我们可以用迭代的方式，从一个初始值出发，不断地更新当前的优化变量，使目标函数下降。

这让求解导函数为零的问题变成了一个不断寻找下降增量Δk的冋题，我们将看到，由于可以对f进行线性化，增量的计算将简单很多。当函数下降直到增量非常小的时候，就认为算收敛，目标函数达到了一个极小值。在这个过程中，问题在于如何找到每次迭代点的增量，而这是一个局部的问题，我们只需要关心f在迭代值处的局部性质而非全局性质。这类方法在最优化、机器学习等领域应用非常广泛。

首先是要进行局部线性化，如果直接将$\min _{\boldsymbol{x}} F(\boldsymbol{x})=\frac{1}{2}\|f(\boldsymbol{x})\|_{2}^{2}$ 按 $F(x)$ 展开，使用一阶泰勒对增量求导就是最速下降法，使用二阶就是牛顿法。

对于后者，有：

$$\Delta \boldsymbol{x}^{*}=\arg \min \left(F(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \Delta \boldsymbol{x}+\frac{1}{2} \Delta \boldsymbol{x}^{\mathrm{T}} \boldsymbol{H} \Delta \boldsymbol{x}\right)$$

$$\boldsymbol{J}+\boldsymbol{H} \Delta \boldsymbol{x}=\mathbf{0} \Rightarrow \boldsymbol{H} \Delta \boldsymbol{x}=-\boldsymbol{J}$$

不过，这两种方法也存在它们自身的问题。最速下降法过于贪心容易走出锯齿路线，反而增加了迭代次数。而牛顿法则需要计算目标数的H矩阵，这在问题规模较大时非常困难，我们通常倾向于避免H的计算。对于一般的问题，一些拟牛顿法可以得到较好的结果，而对于最小二乘问题，还有几类更实用的方法：高斯牛顿法和列文伯格一马夸尔特方法。

高斯牛顿法

同样使用一阶泰勒展开，但是不再对$F(x)$而是对$f(x)$ 展开，这样有：

$$f(\boldsymbol{x}+\Delta \boldsymbol{x}) \approx f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}$$

$$\begin{aligned} \frac{1}{2}\left\|f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}\right\|^{2} &=\frac{1}{2}\left(f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}\right)\left(f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}\right) \\ &=\frac{1}{2}\left(\|f(\boldsymbol{x})\|_{2}^{2}+2 f(\boldsymbol{x}) \boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}+\Delta \boldsymbol{x}^{\mathrm{T}} \boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}\right) \end{aligned}$$

$$\underbrace{\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{J}}_{\boldsymbol{H}(\boldsymbol{x})}(\boldsymbol{x}) \Delta \boldsymbol{x}=\underbrace{-\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} f(\boldsymbol{x})}_{\boldsymbol{g}(\boldsymbol{x})}$$

$$H \Delta x=g$$

这个方程就是正规方程，左侧虽然记成H但并不是二阶Hessian矩阵，只是对它一种近似。

高斯牛顿法优点是相比牛顿法简化计算，收敛快；

缺点是：

• 需要H可逆，但是$JJ^T$ 只半正定=》可能出现奇异矩阵/病态解
• 有可能解出的 $\Delta x$ 太大，这样就不满足准确的局部近似了

// TODO LM与dog-leg法整理

LOAM优化部分推导

构造最小二乘

$$\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{J}(\boldsymbol{x}) \Delta \boldsymbol{x}=-\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{f}(\boldsymbol{x})$$

$J(x)$ 为 n*6的矩阵，这个6即tx,ty,tz,rx,ry,rz

$\Delta x$为最小二乘求解的增量，$f(x)$ 即残差距离。不过，代码会对距离处理一下。

迭代方法：

• 使用本轮给出的tranform初值计算距离残差$f(x)$
• 计算$J(x)$, 求出 $\Delta x$， 利用$\Delta x$ 更新 transform
• 如果$\Delta x$ 的旋转和平移量分别足够小或达到轮数停止迭代，否则根据新的transform重新计算$f(x)$ 循环。

雅可比推导

退化情况处理

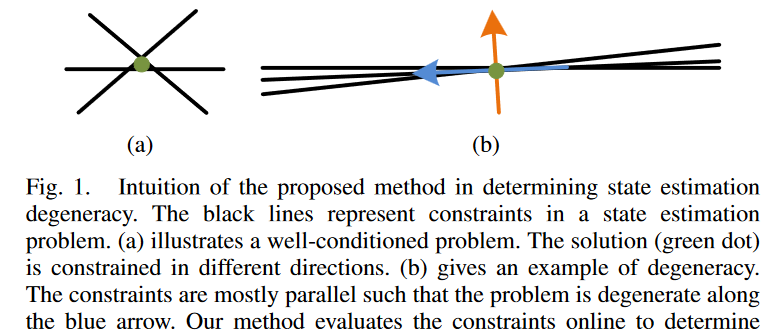
LOAM代码里，优化会根据首先判断出是否退化，如果退化优化更新会另做处理。这源于作者的另一论文 On Degeneracy of Optimization-based State Estimation Problems。

作者指出，在使用视觉传感器时缺少纹理特征、使用激光传感器缺少几何结构信息等情况时，优化问题会退化，这样就算求解出全局最优解，也基本不靠近真实的解，极影响优化方法的可靠性。而观察发现，即便数据局部退化，仍可以尝试用部分约束在问题子空间中求解。由此，作者首先提出了退化因子的概念，配合一个阈值用于检测退化；然后提出了Solution Remapping 的方法，用于加入到优化过程中，从良好方向出分离出去退化方向，优化迭代中只在良好方向上更新（非线性问题的情况），避免得出错误解。

假设A满秩，我们考虑解决如下已经线性化的最小二乘问题：

$$\arg \min _{\boldsymbol{x}}\|\mathbf{A} \boldsymbol{x}-\boldsymbol{b}\|^{2}$$

退化因子的定义

对于下图中已有黑色约束，添加一法线为$\bold{c}$橙色约束:

$$\boldsymbol{c}^{T}\left(\boldsymbol{x}-\boldsymbol{x}_{0}\right)=0,\|\boldsymbol{c}\|=1$$

因其通过原解 $x0$，所以加入新约束后解不变。

接着将新约束沿法线方向移动一个确定距离$\delta d$， 则解会沿c的方向变化 $\delta x_c$ ，尝试 $\bold{c}$ 的各种方向可以找到一个使原解变化最大的方向，这时解变化量记为 $\delta x_c^*$, 我们定义退化因子为：

$$\mathcal{D}=\delta d / \delta x_{c}^{*}$$

数学证明

结论1：对于上面研究的线性系统问题，退化因子只与决定方向的A有关，与初始位置b无关，这和Fig.1.中表现一致。

证明：

分别列出干扰前后带新约束的方程：

$$\left[\begin{array}{c}\mathbf{A} \\ \boldsymbol{c}^{T}\end{array}\right] \boldsymbol{x}=\left[\begin{array}{c}\boldsymbol{b} \\ \boldsymbol{c}^{T} \boldsymbol{x}_{0}\end{array}\right]$$

$$\left[\begin{array}{c}\mathbf{A} \\ \boldsymbol{c}^{T}\end{array}\right] \boldsymbol{x}=\left[\begin{array}{c}\boldsymbol{b} \\ \boldsymbol{c}^{T} \boldsymbol{x}_{0}+\delta d\end{array}\right]$$

下减上得，利用伪逆求得：

$$\delta \boldsymbol{x}=\left(\mathbf{A}^{T} \mathbf{A}+\boldsymbol{c} \boldsymbol{c}^{T}\right)^{-1} \boldsymbol{c} \delta d$$

因为定义了 $\|\boldsymbol{c}\|=1$, x 的变化量可以用 $\delta \boldsymbol{x}$ 向 $\boldsymbol{c}$ 投影得到：

$$\delta x_{c}=\boldsymbol{c}^{T} \delta \boldsymbol{x}=\boldsymbol{c}^{T}\left(\mathbf{A}^{T} \mathbf{A}+\boldsymbol{c} \boldsymbol{c}^{T}\right)^{-1} \boldsymbol{c} \delta d$$

可以看出只与 $\boldsymbol{c}$，$\delta d$ , $\mathbf{A}$ 有关。

结论2：$\mathcal{D}=\lambda_{\min }+1$， $\lambda_{\min } \text {是} \mathbf{A}^{T} \mathbf{A} \text{最小的特征值}$

证明：

因为定义了 $\|\boldsymbol{c}\|=1$， $\boldsymbol{c}$ 的左右伪逆矩阵有 $\boldsymbol{c}_{\mathrm{left}}^{-1}=\left(\boldsymbol{c}^{T} \boldsymbol{c}\right)^{-1} \boldsymbol{c}^{T}=\boldsymbol{c}^{T} \text { and } \boldsymbol{c}_{\mathrm{right}}^{-T}=\boldsymbol{c}\left(\boldsymbol{c}^{T} \boldsymbol{c}\right)^{-1}=\boldsymbol{c}$，代入结论1最后的结果有：

$$\begin{aligned} \delta x_{c} &=\boldsymbol{c}_{\mathrm{left}}^{-1}\left(\mathbf{A}^{T} \mathbf{A}+\boldsymbol{c} \boldsymbol{c}^{T}\right)^{-1} \boldsymbol{c}_{\mathrm{right}}^{-T} \delta d \\ &=\left(\boldsymbol{c}^{T}\left(\mathbf{A}^{T} \mathbf{A}+\boldsymbol{c} \boldsymbol{c}^{T}\right) \boldsymbol{c}\right)^{-1} \delta d \\ &=\left(\boldsymbol{c}^{T} \mathbf{A}^{T} \mathbf{A} \boldsymbol{c}+1\right)^{-1} \delta d \end{aligned}$$

要得到退化因子，就要让$\delta x_c$ 最大，所以有：

$$\boldsymbol{c}^{*}=\arg \min \boldsymbol{c}^{T} \mathbf{A}^{T} \mathbf{A} \boldsymbol{c}, \text { s.t. }\|\boldsymbol{c}\|=1$$

等价于：

$$\boldsymbol{c}^{*}=\arg \min _{\boldsymbol{c}} \frac{\boldsymbol{c}^{T} \mathbf{A}^{T} \mathbf{A} \boldsymbol{c}}{\boldsymbol{c}^{T} \boldsymbol{c}}$$

根据Rayleigh quotient, 由于$\mathbf{A}^{T} \mathbf{A}$ 是实对称矩阵，则上式右侧的最小值就等于$\mathbf{A}^{T} \mathbf{A}$ 的最小特征值，因此：

$$\delta x_{c}^{*}=\frac{\delta d}{\lambda_{\min }+1}$$

$$\mathcal{D}=\delta d / \delta x_{c}^{*}=\lambda_{\min }+1$$

最小特征值对应特征向量的方向是第一大的可能退化方向，由于实对称矩阵$\mathbf{A}^{T} \mathbf{A}$ 特征向量相互正交，根据Rayleigh quotient，得出每个特征向量的方向的退化因子就是相应的特征值 +1 ，它们就是第$i$个退化方向。（？）

Solution Remapping

算法

设$\mathbf{A}^{T} \mathbf{A}$小于一个退化阈值的 特征值数量为$m, 0 \leq m \leq n$，$m=0$为完全良好的问题，$m=n$为完全退化。

构造如下矩阵用于分离方向：

$$\begin{aligned} \mathbf{V}_{p} &=\left[\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{m}, 0, \ldots, 0\right]^{T} \\ \mathbf{V}_{u} &=\left[0, \ldots, 0, \boldsymbol{v}_{m+1}, \ldots, \boldsymbol{v}_{n}\right]^{T} \\ \mathbf{V}_{f} &=\left[\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{m}, \boldsymbol{v}_{m+1}, \ldots, \boldsymbol{v}_{n}\right]^{T} \end{aligned}$$

$x_p$ 定义为一个预测值，$x_u$是求解方程后得到观测更新值，$x_f$为最终给出的解。这里借鉴了Kalman滤波的概念。

我们让预测值投影到退化方向，更新值投影到未退化方向，综合两部分得到最终的解，如上图所示。

$$\boldsymbol{x}_{p}^{\prime}=\mathbf{V}_{f}^{-1} \mathbf{V}_{p} \boldsymbol{x}_{p} \text { and } \boldsymbol{x}_{u}^{\prime}=\mathbf{V}_{f}^{-1} \mathbf{V}_{u} \boldsymbol{x}_{u}$$

（原来就是把右侧逆拿到左边，可以从投影/变换的角度理解。）

最后合成两部分：

$$\boldsymbol{x}_{f}=\boldsymbol{x}_{p}^{\prime}+\boldsymbol{x}_{u}^{\prime}$$

对于实际非线性问题，算法如下：

其他：

文章中采集了退化与非退化场景的最小特征值，取边界中值作为阈值。

论文中说，根据经验只需要在迭代开始确定退化方向，没必要每轮都更新。除此之外，只在非退化方向上更新，舍弃了退化方向的更新。

LOAM代码中退化处理

if (iterCount == 0) {
    //特征值1*6矩阵
    cv::Mat matE(1, 6, CV_32F, cv::Scalar::all(0));
    //特征向量6*6矩阵
    cv::Mat matV(6, 6, CV_32F, cv::Scalar::all(0));
    cv::Mat matV2(6, 6, CV_32F, cv::Scalar::all(0));

    //求解特征值/特征向量
    cv::eigen(matAtA, matE, matV);
    matV.copyTo(matV2);

    isDegenerate = false;
    //特征值取值门槛
    float eignThre[6] = {10, 10, 10, 10, 10, 10};
    for (int i = 5; i >= 0; i--) {//从小到大查找
        if (matE.at<float>(0, i) < eignThre[i]) {//特征值太小，则认为处在兼并环境中，发生了退化
            for (int j = 0; j < 6; j++) {//对应的特征向量置为0
                matV2.at<float>(i, j) = 0;
            }
            isDegenerate = true;
        } else {
            break;
        }
    }

    //计算P矩阵
    matP = matV.inv() * matV2;
}

if (isDegenerate) {//如果发生退化，只使用预测矩阵P计算
    cv::Mat matX2(6, 1, CV_32F, cv::Scalar::all(0));
    matX.copyTo(matX2);
    matX = matP * matX2;
}

第一轮迭代时判断是否退化，如果退化，每次用$\mathbf{V}_{f}^{-1} \mathbf{V}_{u} \Delta \boldsymbol{x}_{u}$ 更新。

结语

至此，LOAM终于学习完了，接下来可能看看Lego LOAM,LIO等。

参考

[1] J. Zhang和S. Singh, 《LOAM: Lidar Odometry and Mapping in Real-time》, 发表于 Robotics: Science and Systems 2014, 7月 2014. doi: 10.15607/RSS.2014.X.007.

[2] J. Zhang, M. Kaess和S. Singh, 《On degeneracy of optimization-based state estimation problems》, 收入 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 5月 2016, 页 809–816. doi: 10.1109/ICRA.2016.7487211.

[3] 基于 LOAM 的方法中平面点和边缘线的残差构建以及雅可比推导

[4] 矩阵求导总结（二） | Dwzb’s Blog

[5] LOAM后端优化算法分析 - 知乎

[6] https://github.com/soloice/Matrix_Derivatives

[7] 矩阵求导术（上） - 知乎

[8 矩阵求导术（下） - 知乎

[9] Matrix calculus - Wikipedia

[10] Rayleigh quotient